En artículos anteriores, se mencionó que existen dos formas diferentes de conectar dos o más dispositivos eléctricos entre sí en un circuito. Pueden conectarse mediante conexiones en serie o mediante conexiones en paralelo.
Cuando todos los dispositivos de un circuito están conectados mediante conexiones en serie, el circuito se denomina circuito en serie. Cuando todos los dispositivos de un circuito están conectados mediante conexiones en paralelo, el circuito se denomina circuito en paralelo.
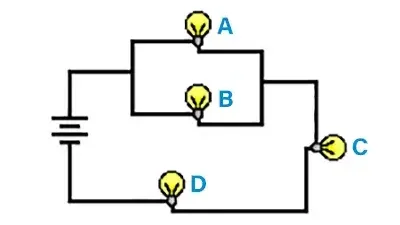
Un tercer tipo de circuito implica el uso combinado de conexiones en serie y en paralelo en un circuito; dichos circuitos se denominan circuitos mixtos, circuitos combinados o conexiones mixtas.
El circuito de la derecha es un ejemplo del uso de conexiones en serie y en paralelo en un mismo circuito. En este caso, las bombillas A y B están conectadas en paralelo y las bombillas C y D en serie. Es un ejemplo de circuito combinado.
Cuando se analizan circuitos combinados, es muy importante tener una sólida comprensión de los conceptos que pertenecen tanto a los circuitos en serie como a los circuitos en paralelo. Dado que en los circuitos combinados se utilizan ambos tipos de conexiones, los conceptos asociados a ambos tipos de circuitos se aplican a las partes respectivas del circuito. Los principales conceptos asociados a los circuitos en serie y en paralelo se organizan en la siguiente tabla.
| Circuitos en Serie | Circuitos en Paralelo |
|---|---|
| La corriente es la misma en todos los resistores; esta corriente es igual a la de la batería. | La caída de voltaje es la misma en cada rama paralela. |
| La suma de las caídas de voltaje en los resistores individuales es igual al voltaje nominal de la batería. | La suma de la corriente en cada rama individual es igual a la corriente fuera de las ramas. |
| La resistencia total del conjunto de resistores es igual a la suma de los valores de resistencia individuales, Rtot = R1 + R2 + R3 + … | La resistencia equivalente o total del conjunto de resistores viene dada por la ecuación, 1/Req = 1/R1 + 1/R2 + 1/R3 … |
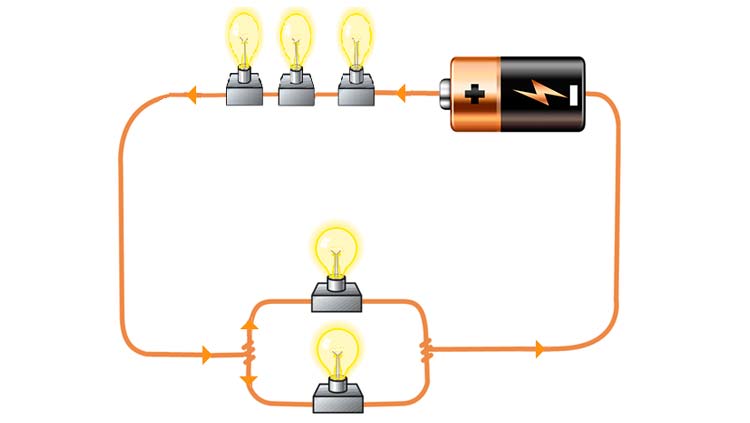
Cada uno de los conceptos anteriores tiene una expresión matemática. Combinando las expresiones matemáticas de los conceptos anteriores con la ecuación de la ley de Ohm (ΔV = I * R) se puede realizar un análisis completo de un circuito mixto.
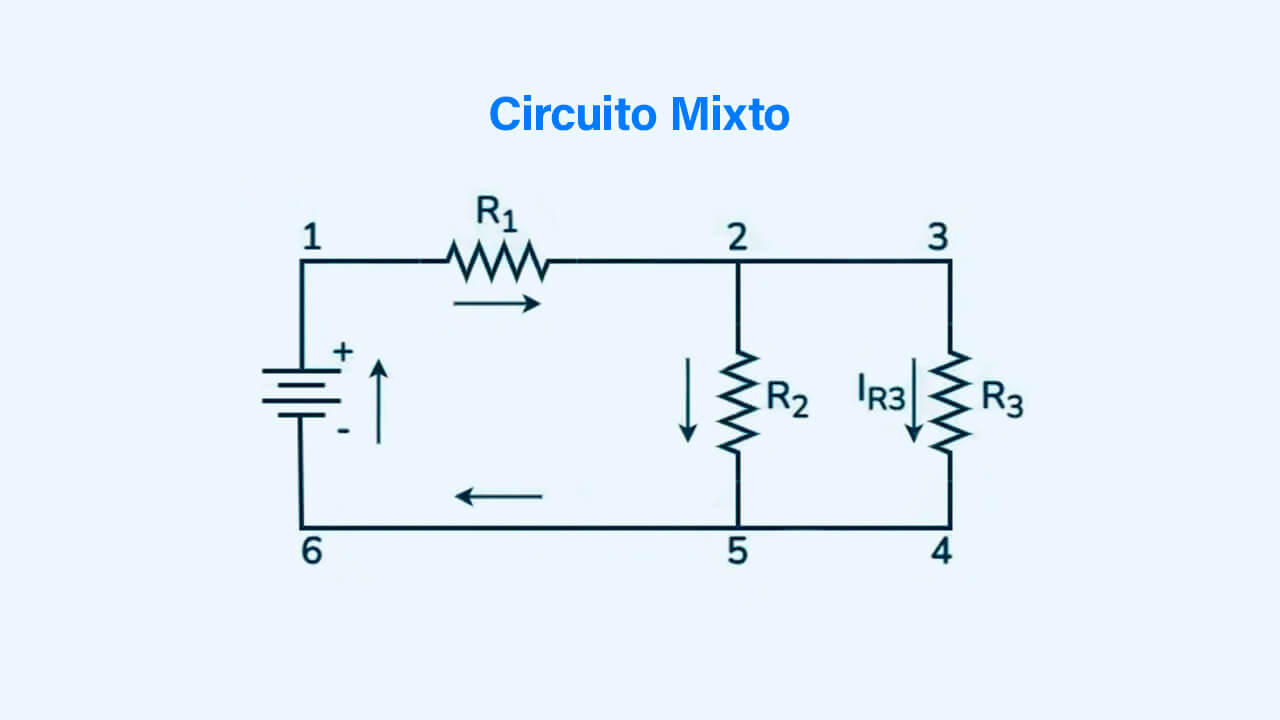
¿Qué es un Circuito Mixto?
Un circuito mixto, o circuito combinado, es un tipo de circuito conectado tanto en serie como en paralelo. Todos los elementos de este circuito están conectados de extremo a extremo.
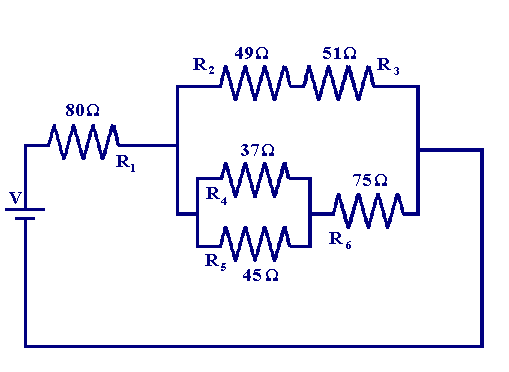
El circuito que se muestra arriba es un ejemplo del uso de una conexión en mixto dentro de un circuito.
Características de un Circuito Mixto
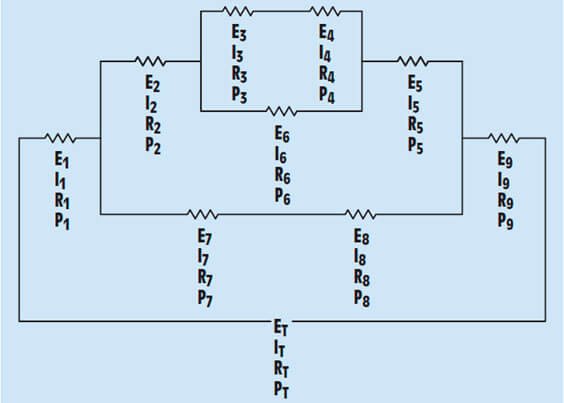
Las características del Circuito Mixto son las siguientes:
- Se caracteriza por estar compuesta por la combinación de circuitos en serie y paralelo.
- El voltaje varia dependiendo de la caida de tensión entre cada nodo.
- La intensidad de la corriente varía dependiendo de la conexión.
- Existen dos formulas para calcular la resistencia total del circuito mixto.
¿Cómo Resolver un Circuito Mixto?
El siguiente ejemplo es el caso más fácil para calcular un circuito mixto: los resistores colocadas en paralelo tienen la misma resistencia. El objetivo del análisis es determinar la corriente y el voltaje en cada resistor.
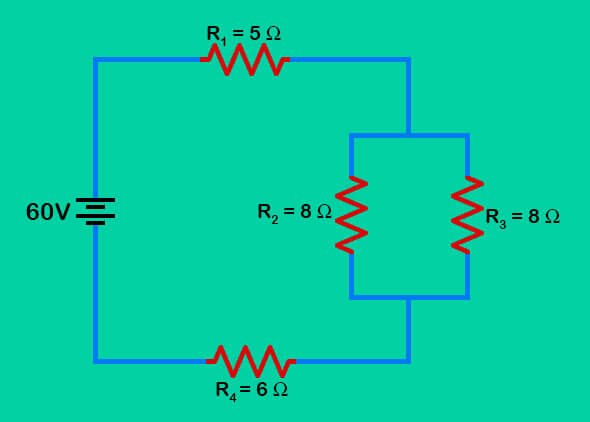
Calculando la Resistencia Total de un Circuito Mixto
Como ya sabemos, el primer paso es simplificar el circuito reemplazando las dos resistencias paralelas con una sola resistencia que tenga una resistencia equivalente. Dos resistencias de 8 Ω en serie son equivalentes a una sola resistencia de 4 Ω. Por lo tanto, las dos resistencias de ramificación (R2 y R3) se pueden reemplazar por una sola resistencia equivalente a 4 Ω. Esta resistencia de 4 Ω está en serie con R1 y R4. Por lo tanto, la resistencia total es:
RTot = R1 + 4 Ω + R4 = 5 Ω + 4 Ω + 6 Ω
RTot = 15 Ω
Cómo Calcular la Corriente Total de un Circuito Mixto
Ahora se puede usar la ecuación de la Ley de Ohm (ΔV = I • R) para determinar la corriente total en el circuito. Al hacerlo, deberá usarse la resistencia total y el voltaje total (o voltaje de la batería).
ITot = ΔVTot / RTot = (60 V) / (15 Ω)
ITot = 4 Amp
El cálculo de corriente de 4 amperios representa la corriente en la ubicación de la batería. Sin embargo, las resistencias R1 y R4 están en serie y la corriente en resistencias conectadas en serie es igual en todas partes. Así,
ITot = I1 = I4 = 4 Amp
Para ramas paralelas, la suma de la corriente en cada rama individual es igual a la corriente fuera de las ramas. Por lo tanto, I2 + I3 debe ser igual a 4 Amp. Hay un número infinito de valores posibles de I2 e I3 que satisfacen esta ecuación. Como los valores de resistencia son iguales, los valores actuales en estas dos resistencias también son iguales. Por lo tanto, la corriente en las resistencias 2 y 3 es igual a 2 Amp.
I2 = I3 = 2 Amp
Calculando el Voltaje utilizando la Ley de Ohm
Ahora que se conoce la corriente en cada ubicación de resistencia individual, se puede usar la ecuación de la ley de Ohm (ΔV = I • R) para determinar la caída de voltaje en cada resistencia. Estos cálculos se muestran a continuación.
ΔV1 = I1 • R1 = (4 Amp) • (5 Ω)
V1 = 20 V
ΔV2 = I2 • R2 = (2 Amp) • (8 Ω)
V2 = 16 V
ΔV3 = I3 • R3 = (2 Amp) • (8 Ω)
V3 = 16 V
ΔV4 = I4 • R4 = (4 Amp) • (6 Ω)
V4 = 24 V
Ejemplos Resueltos de Circuitos Mixtos
De la siguiente figura calcularemos todas las magnitudes eléctricas del circuito mixto de resistencias
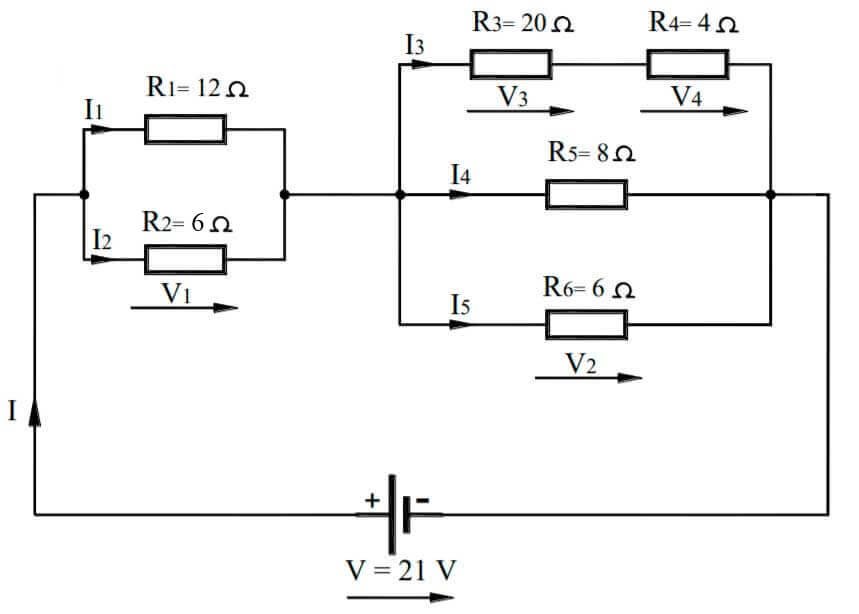
Comenzaremos por calcular la resistencia equivalente de todo el circuito (Req).
Inicialmente sustituiremos, por un lado, R1 y R2 por su equivalente, y por otro, R3 y R4 por la resistencia equivalente de ambas.
Dado que R1 y R2 están en paralelo, su equivalente será:
R1,2 = 1/(1/R1 + 1/R2) = 1/(1/12 + 1/6) = 4Ω
El equivalente de R3 y R4, al estar en serie es el siguiente:
R3,4 = R3 + R4 = 20 + 4 = 24Ω
El circuito queda simplificado de la siguiente forma:
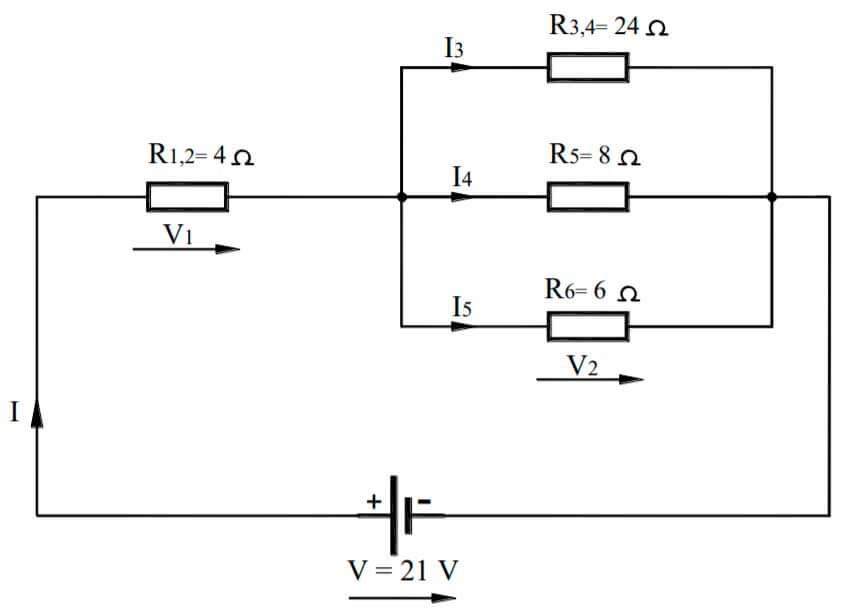
A continuación calculamos la resistencia equivalente de R3,4 , R5 y R6 , y dado que están en paralelo tendremos:
R2a6 = 1/(1/R3,4 + 1/R5 + 1/R6) = 1/(1/24 + 1/8 + 1/6) = 3Ω
el circuito queda de la siguiente forma:
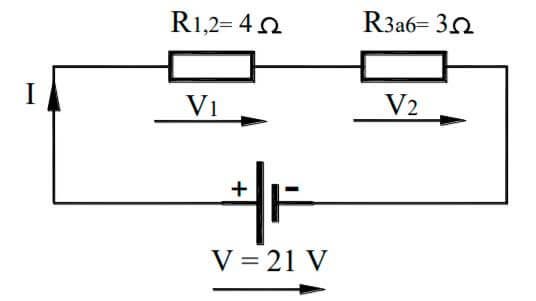
Finalmente calculamos la resistencia equivalente del circuito, para lo cual sumamos el valor de R1,2 y R3a6, puesto que están en serie.
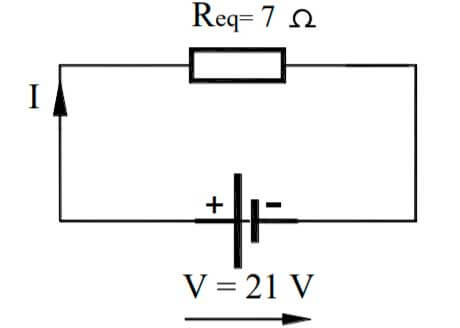
Req = R1,2 + R3a6 = 4 + 3 = 7Ω
El circuito final simplificado es el que se muestra en la siguiente figura:
Deja una respuesta