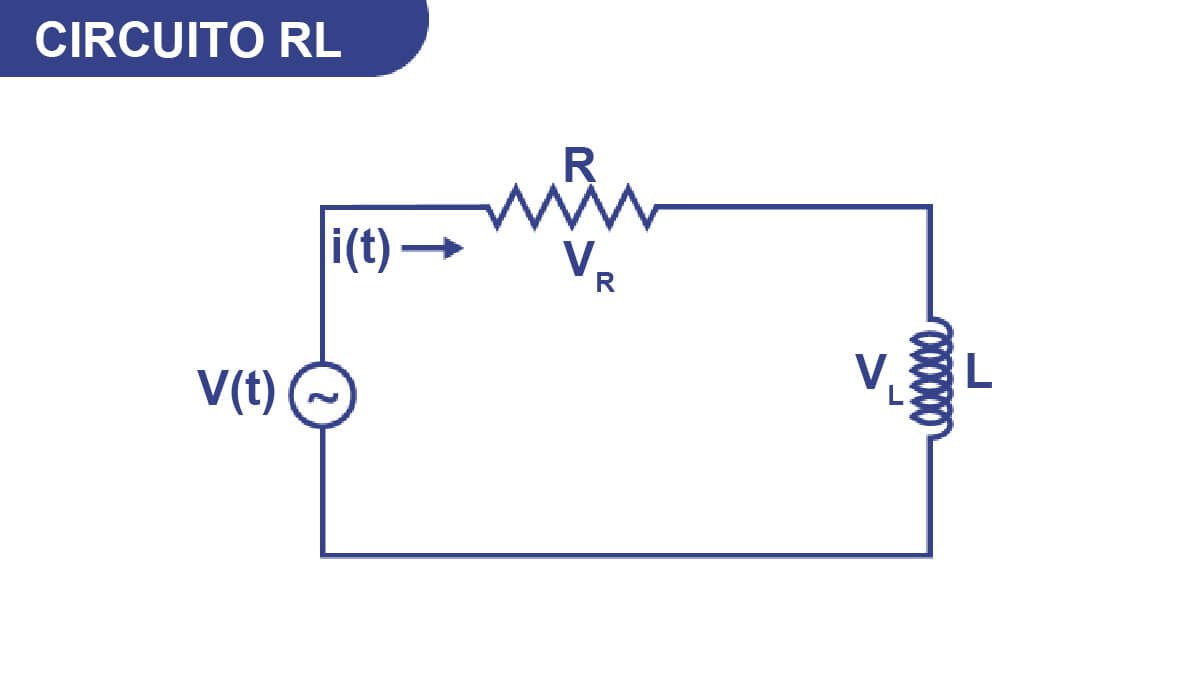
Los tres elementos básicos de los circuitos lineales son el resistor, el condensador y el inductor. En este artículo veremos las características de los circuitos formados por un resistor y un inductor en serie (circuitos RL). Nos centraremos principalmente en la respuesta de un circuito RL a una tensión escalonada y a una onda cuadrada de tensión.
Un circuito RL, también denominado circuito resistor-inductor, desempeña un papel fundamental en la ingeniería eléctrica y en los elementos inductivos. En este circuito intervienen un resistor (R) y un inductor (L) dispuestos en serie o en paralelo.
El resistor convierte la energía eléctrica en calor al resistir el flujo de corriente, mientras que el inductor almacena energía en su campo magnético. La inductancia del inductor (medida en henrys) se denota por «L» y es indicativa de la intensidad del campo magnético, influida por la velocidad de cambio de la corriente.
Al aplicar tensión a un circuito RL, la corriente no aumenta instantáneamente, a diferencia de lo que ocurre en un circuito puramente resistivo. En cambio, el inductor resiste los cambios de corriente, lo que provoca una respuesta retardada en el circuito.
La constante de tiempo (τ) del circuito RL, calculada como la relación entre la inductancia y la resistencia (τ = L/R), significa el tiempo necesario para que la corriente alcance alrededor del 63.2% de su valor final durante un estado transitorio.
Comprender los comportamientos transitorios y estacionarios es esencial para los ingenieros encargados de diseñar circuitos que cumplan criterios de rendimiento específicos.
Te Puede Interesar: Componentes de un circuito eléctrico ¿Qué es un diagrama de circuito? ¿Qué es el circuito integrado? Diferencia entre circuito en serie y paralelo¿Qué es un Circuito RL?
Un circuito RL (también conocido como filtro RL, circuito resistor-inductor o red RL) es un tipo de circuito eléctrico que consta de rudimentos resistivos (R) e inductivos (L). Los factores cruciales son un resistor (R) y un inductor (L) conectados en serie o en paralelo. Estos circuitos son básicos en ingeniería eléctrica y resultan esenciales para comprender la estructura de los sistemas eléctricos.
A continuación se explican brevemente los rudimentos cruciales en un circuito RL
- Resistor (R): La resistencia de un material depende de su tipo y forma. Cuando la corriente eléctrica pasa a través de él, el material convierte parte de la energía eléctrica en calor. La resistencia cuantifica el obstáculo al paso de la corriente en un circuito eléctrico y se expresa en ohmios, simbolizados por la letra griega omega (Ω).
- Inductor (L): Un inductor es un elemento de circuito de dos terminales que almacena energía en su campo magnético. Los inductores se suelen fabricar enrollando alambre en una bobina. Un inductor es un elemento eléctrico no resistente que almacena energía en su propio campo cuando la corriente lo atraviesa. Una unidad es el Henry (H).
Los circuitos RL suelen encontrarse en diversos sistemas electrónicos, como contaminantes, fabricas e inventarios de energía.
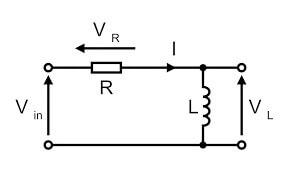
Considere el siguiente circuito RL que incluye un resistor y un inductor usando una fuente de voltaje. Creemos que el flujo de corriente dentro del circuito es I (amperio) y a través de la resistencia es IR y el inductor es IL correspondientemente.
Dado que tanto los componentes como R & L están conectados en serie, entonces el flujo de corriente dentro de ambos componentes y el circuito completo será el mismo como IR = IL = I. La caída de voltaje a través de la resistencia y el inductor son VR y VI
Aplicando la ley de voltaje de Kirchhoff (es decir, la suma de la caída de voltaje debe ser igual para aplicar voltaje) a este circuito obtenemos,
Una vez que se aplica la ley de voltaje de Kirchhoff al circuito anterior, obtenemos
V = VR + VL
Factor de potencia
El circuito RL o circuito resistor-inductor es un tipo de circuito eléctrico que se puede construir con resistores e inductores que están conectados a una fuente de voltaje o corriente. Un circuito RL de primer orden comprende principalmente un resistor y un inductor para formar un circuito RL. El factor de potencia de este circuito es bajo debido a la carga inductiva como un motor de inducción trifásico. Incluso las lámparas, los transformadores y los dispositivos de soldadura funcionan con factores de potencia retardados bajos.
Circuito RL en serie
En un circuito RL en serie, el flujo de corriente se retrasa con respecto al voltaje a través de un ángulo «ϕ» debido al efecto inductor. Entonces, aquí, el factor de potencia se puede dar como el coseno del ángulo de retraso «ϕ»
El factor de potencia = Cos ϕ = Resistencia/Impedancia = R/Z
Cos ϕ = R/√R2+XL2 = R/√R2+ (ω L)2
La ecuación anterior se puede dividir con «R»
Cos ϕ = 1/√1+ (ω L/R)2
De hecho, cuando tenemos ω L>>R, que es un factor de potencia pequeño, el «1» en el denominador se vuelve insignificante.
Entonces, Cos ϕ = R / ω L
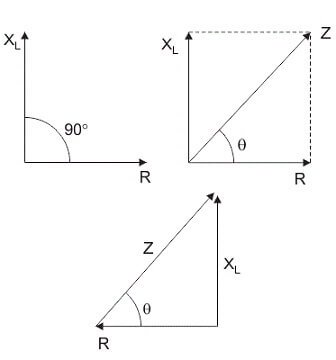
Diagrama Fasorial del circuito RL en serie
El diagrama fasorial del circuito RL en serie se muestra a continuación:

Los siguientes pasos dan instrucciones paso a paso para dibujar el diagrama fasorial.
Aquí, la corriente (I) se puede tomar como referencia.
El VR que se conoce como la caída de voltaje a través de la resistencia = IR se puede dibujar dentro de la fase a través de la corriente (I).
A través de la reactancia inductiva, la caída de voltaje es VL = IXL se puede dibujar por delante del flujo de corriente porque el flujo de corriente retrasa el voltaje a través de 90 grados dentro del circuito inductivo.
Las caídas de la suma vectorial de dos voltajes son VR y VL, que son equivalentes al voltaje V dado.
Entonces,
En el triángulo anterior como OAB
VR = IR y VL = IXL donde XL = 2πfLRL
V = √(VR)2+ (VL)2
= √(IR)2+ (IXL)2
= I è2+ (XL)2
I = L = V/Z
Z = √R2 + XL2
Aquí, «Z» es toda la resistencia que se ofrece al flujo de CA a través de un circuito RL en serie. Entonces se conoce como la impedancia del circuito RL y se mide en ohmios (Ω).
Ángulo de Fase
En un circuito RL en serie, el flujo de corriente se retrasa con respecto al voltaje con un ángulo de 90° y se denomina ángulo de fase.
ϕ = tan-1 (XL/R)
La Impedancia del Circuito RL en serie
La impedancia del circuito RL en serie se opone al flujo de corriente y no es más que la combinación del efecto de resistencia (R) y reactancia inductiva (XL) de todo el circuito. La impedancia «Z» en ohmios se puede dar de la siguiente manera.
Z = (R2 + XL2)0.5
Desde el triángulo de ángulo recto en las siguientes imágenes, ángulo de fase ϕ = tan-1 (XL / R).
Circuito RL en Paralelo
Cuando tanto el resistor como el inductor están conectados en paralelo entre sí y se alimentan a través de una fuente de voltaje, se conoce como circuito RL paralelo. Los voltajes de entrada y salida del circuito son Ve y Vs. Una vez que el resistor y el inductor están conectados en paralelo, Ve es equivalente a Vs. Sin embargo, el flujo de corriente dentro de estos componentes no es el mismo.
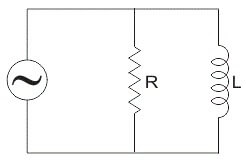
Este tipo de circuito no se puede utilizar como filtro para voltajes porque los voltajes de entrada y salida en este circuito son iguales. Entonces, debido a esta razón, este circuito no se usa con frecuencia como se evalúa para el circuito RL en serie.
Diagrama Fasorial de un circuito RL en paralelo
En un circuito RC en paralelo, la relación principal entre el voltaje y las corrientes se puede ilustrar mediante el diagrama vectorial (fasor).
- El vector de referencia «E» significa el voltaje dentro del circuito paralelo RL.
- Como el flujo de corriente a través de la resistencia está dentro de la fase por el voltaje a través de él, entonces se muestra IR en el vector de voltaje.
- El «IL» retrasa el voltaje en un ángulo de 90 grados y se puede colocar dentro de una dirección hacia abajo para retrasar el vector de voltaje en un ángulo de 90 grados.
- Aquí, tanto la suma de vectores como IR e IL proporcionan un resultado que significa la suma (IT) de lo contrario, la corriente de línea
- El ángulo «θ» denota la fase entre la corriente y el voltaje de línea dados.
- El diagrama fasorial del circuito RL paralelo se muestra a continuación.
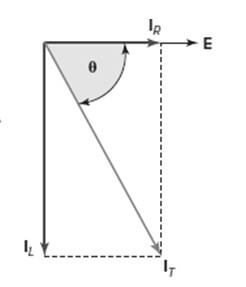
En el caso de un circuito en paralelo, el flujo de corriente dentro de cada rama de un circuito funciona independientemente de las corrientes dentro de las ramas restantes. El flujo de corriente en cada rama puede determinarse a través del voltaje en la rama y la resistencia al flujo de corriente en forma de reactancia inductiva o resistencia incluida en la rama.
La corriente en la rama individual se puede determinar mediante la ley de ohmios.
IR = E/R
IL = E/XL
El flujo de corriente dentro de la rama resistiva incluye una fase similar a la tensión dada; sin embargo, la corriente en una rama inductiva se retrasa respecto a la tensión dada con 90 grados de ángulo. En consecuencia, toda la corriente de la línea incluye IR e IL con 90 grados de desfase entre sí.
El flujo de corriente en ambos componentes puede formar los catetos de un triángulo rectángulo y la corriente total es la hipotenusa. Por lo tanto, el teorema de Pitágoras se utiliza para incluir estas corrientes juntas mediante el uso de la siguiente ecuación:
IT = √IR2 + IL2
En estos circuitos, el ángulo de fase en el que toda la corriente va por detrás de la tensión está entre 0 y 90 grados. Por lo tanto, el tamaño del ángulo se puede determinar a través de si hay una corriente inductiva adicional o una corriente resistiva.
Si hay una corriente inductiva adicional, entonces el ángulo de fase ‘θ’ estará más cerca de los 90 grados. Será más cercano a cero grados si hay una corriente resistiva adicional. Por lo tanto, a partir del diagrama vectorial del circuito anterior podemos observar que el valor del ángulo de fase se puede medir a partir de la siguiente ecuación:
Θ = tan-1 (IL/IR)
Impedancia de un circuito RL en paralelo
La impedancia de un circuito RL en paralelo puede definirse como la resistencia total hacia el flujo de corriente. Comprende la resistencia que se ofrece desde la rama resistiva ‘R’ así como la reactancia inductiva ‘XL’ puede ofrecerse a través de la rama inductiva.
La impedancia del circuito RL en paralelo puede calcularse como un circuito resistivo en paralelo. Pero, como R y XL son cantidades vectoriales, deben incluirse vectorialmente. En consecuencia, la ecuación de impedancia de un circuito RL paralelo incluye un solo resistor e inductor, por lo que la fórmula de impedancia para un circuito RL paralelo es
Z = RXL/√R2 + XL2
En el denominador de la ecuación anterior es la suma vectorial de la resistencia & la resistencia de la inductancia. Así que si hay más de una rama de resistiva & la inductiva, deben ser equivalentes para todas las resistencias de lo contrario la reactancia de estas ramas paralelas.
Una vez que la corriente total y el voltaje aplicado son bien conocidos, entonces la impedancia puede ser medida más simplemente usando la ley de Ohm como la siguiente.
Z = E/IT
La impedancia del circuito RL paralelo es siempre baja en comparación con la resistencia o la reactancia inductiva de cualquier rama. Debido a esto es la razón, cada rama forma un carril separado para el flujo de la corriente, por lo que disminuye la resistencia del circuito completo hacia el flujo de corriente.
Cuando la rama tiene la mayor cantidad de corriente por lo que tiene el mayor efecto sobre el ángulo de fase. Por lo tanto, esto es inverso a un circuito RL en serie.
En un circuito RL paralelo, si la inductancia es mayor que la resistencia, entonces la corriente de rama resistiva es superior en comparación con la corriente de rama inductiva. En consecuencia, el ángulo de fase entre el voltaje dado y toda la corriente puede estar más cerca de 0 grados porque responde mejor en la naturaleza.
Ventajas de los circuitos RL
- Almacén de energía: Los inductores de los circuitos RL almacenan energía en sus propios campos. Esta energía puede liberarse cuando se necesite, lo que hace que los circuitos RL sean útiles en operaciones en las que el almacenamiento y la liberación de energía son esenciales.
- Ventaja de filtrado: Los circuitos RL pueden funcionar como filtros de paso bajo, permitiendo el paso de señales de baja frecuencia a la vez que atenúan las señales de alta frecuencia. Esto resulta ventajoso en aplicaciones que requieren la eliminación de ruidos de alta frecuencia.
- Transiciones de corriente suaves: Cuando los inductores de alta frecuencia repelen los cambios de corriente, lo que da lugar a transiciones suaves en la entrada de corriente. Esta característica es crucial en situaciones en las que se requiere un cambio suave de la corriente.
Desventajas de los circuitos RL
- Complejidad: los circuitos RL pueden ser más difíciles de entender y construir que los circuitos que sólo tienen resistores o condensadores. La adición de inductores hace que las ecuaciones sean más complejas, lo que puede dificultar el análisis.
- Fuerza electromotriz inversa: Cuando la corriente que circula por un inductor cambia, produce una fuerza electromotriz (FEM) que resiste el cambio. Esto puede provocar un pico de tensión y requerir circuitos adicionales de protección.
- Pérdidas de potencia: Los circuitos RL pueden sufrir pérdidas de potencia, especialmente en forma de pérdidas resistivas en el devanado de la bobina. Estas pérdidas pueden reducir la eficacia global del circuito.
Usos del circuito RL
Los componentes básicos como los resistores, los condensadores y los inductores se combinan para formar diferentes circuitos como los circuitos RC, RL y RLC. Las aplicaciones de los circuitos RL, RC y RLC son las siguientes.
- Amplificadores de RF
- Sistemas de comunicación
- Circuitos de filtrado
- Procesamiento de señal
- Circuitos de oscilación
- Aumento de la corriente o la tensión
- Circuitos de sintonía variable
- Transmisores de ondas de radio
- Circuito LC Resonante/Circuito RLC
- Estos circuitos se utilizan como fuentes de alimentación de CC dentro de los amplificadores de RF porque el inductor (L) se utiliza para suministrar corriente de polarización de CC y bloquear la RF para que llegue a la fuente de alimentación.
Por lo tanto, este artículo da a conocer una descripción general sobre el Circuito RL, el circuito RL en serie, el circuito RL en paralelo, el diagrama fasorial y sus usos. Aquí hay una pregunta para usted, ¿Cuáles son las ventajas de los circuitos RL?
PREGUNTAS FRECUENTES
El factor de potencia de un circuito RL es la relación entre la potencia real disipada y la potencia aparente.
Los circuitos RL se utilizan en sistemas de comunicación, transmisores de ondas de radio, circuitos osciladores, amplificadores de RF, circuitos de filtrado, circuitos de sintonía variable, aumento de corriente y tensión, etc.
Un circuito RL es un circuito formado por componentes pasivos, como el resistor y el inductor, conectados entre sí y accionados por una fuente de corriente o de tensión.
La reactancia inductiva (XL) es la resistencia que ofrece un inductor a la corriente alterna. Varía en proporción tanto a la frecuencia de la señal alterna como a la inductancia de la bobina.