¿Qué es binario?
El binario describe un esquema de numeración en el que sólo hay dos valores posibles para cada dígito — 0 ó 1 — y es la base de todos los códigos binarios utilizados en los sistemas informáticos. Estos sistemas utilizan este código para comprender las instrucciones operativas y las entradas del usuario y para presentar una salida relevante al usuario.
El término binario también se refiere a cualquier sistema de codificación/descodificación digital en el que existen exactamente dos estados posibles. En la memoria, el almacenamiento, el procesamiento y las comunicaciones de datos digitales, los valores 0 y 1 a veces se denominan bajo y alto, respectivamente. En los transistores, 1 se refiere a un flujo de electricidad, mientras que 0 representa la ausencia de flujo de electricidad.

Explicación del sistema binario
El sistema de numeración binario fue perfeccionado en el siglo XVII por Gottfried Leibniz. En matemáticas y en sistemas informáticos, un dígito binario, o bit, es la unidad de datos más pequeña. Cada bit tiene un único valor, 1 ó 0, lo que significa que no puede tomar ningún otro valor.
Las computadoras pueden representar números utilizando código binario en forma de 1s y 0s digitales dentro de la unidad central de procesamiento (CPU) y la RAM. Estos números digitales son señales eléctricas que se activan o desactivan dentro de la CPU o la RAM.
Binario vs decimal
Dado que el sistema binario utiliza sólo dos dígitos o bits y representa los números mediante patrones variables de 1s y 0s, se conoce como sistema de base-2. Aquí, 1 se refiere a «encendido» o «verdadero», mientras que 0 se refiere a «apagado» o «falso».
En cambio, el sistema de numeración decimal es un sistema de base-10, en el que cada lugar posible en un número puede ser uno de 10 dígitos (0-9). En un número de varios dígitos, el dígito situado más a la derecha ocupa el primer lugar, el dígito situado a su izquierda ocupa el lugar 10, el dígito situado más a la izquierda ocupa el lugar 100 y así sucesivamente.
Ejemplo
En el número de cuatro dígitos 1980, éstos son los lugares ocupados por cada dígito.
| 1 | 9 | 8 | 0 |
| lugar 1000 | lugar 100 | lugar 10 | lugar 1 |
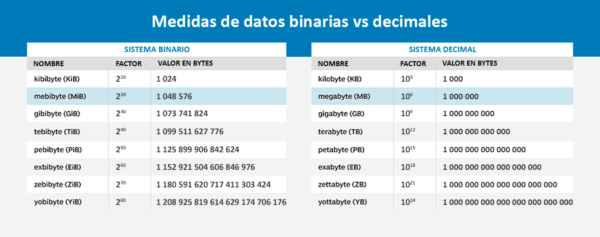
Importancia del código binario
El sistema numérico binario es la base de todos los sistemas y operaciones informáticos. Permite a los dispositivos almacenar, acceder y manipular todo tipo de información dirigida hacia y desde la CPU o la memoria. Esto hace posible el desarrollo de aplicaciones que permiten a los usuarios hacer lo siguiente:
- ver sitios web
- crear y actualizar documentos
- jugar;
- ver vídeos en streaming y otros tipos de información gráfica;
- acceder a programas informáticos
- realizar cálculos y análisis de datos.
El esquema binario de 1s y 0s digitales ofrece una forma sencilla y elegante de que funcionen las computadoras. También permite controlar circuitos lógicos y detectar los estados verdadero (1) y falso (0) de una señal eléctrica.
Cómo funcionan los números binarios
El sistema binario es el lenguaje principal de los sistemas informáticos. En estos sistemas, un número binario está formado por una serie de ocho bits. Esta serie se conoce como byte. En el esquema binario, la posición de cada dígito determina su valor decimal. Así, entendiendo la posición de cada bit, un número binario puede convertirse en un número decimal.
En los números decimales, cada posición adicional se multiplica por 10 a medida que nos desplazamos de derecha a izquierda (posición 1, posición 10, posición 100, etc.). Sin embargo, en los números binarios, cada lugar adicional al desplazarnos de derecha a izquierda se multiplica por dos. Los dos ejemplos siguientes explican esta idea.
Ejemplo 1
Así es como se calculan los valores decimales para un número binario de 8 bits (byte) 01101000.
En este número, el primer dígito está en el extremo derecho, mientras que el octavo dígito está en el extremo izquierdo. Los dígitos del segundo (0) al séptimo (1) se leen de derecha a izquierda.
| Posición del bit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Bit | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| Cálculo de binario-a-decimal (exponente) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| Valor decimal (x2) | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
A medida que la posición del bit aumenta de uno a ocho, el valor decimal anterior se multiplica por dos. Por eso el primer bit tiene un valor de 1, el segundo bit tiene un valor de 2, el tercer bit tiene un valor de 4 y así sucesivamente.
El valor final del número decimal se calcula sumando los valores individuales de la tabla anterior. Sin embargo, sólo deben sumarse los valores en los que el bit es igual a 1. Estos valores representan la posición «encendido». Los 0 representan la posición «apagado», por lo que no se tienen en cuenta en el cálculo del valor decimal.
Así, para el número binario 01101000, el valor decimal se calcula de la siguiente manera:
8 + 32 + 64 = 104
Ejemplo 2
A continuación se muestra cómo se calculan los valores decimales para el número binario 11111111.
| Posición del bit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Bit | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Cálculo de binario-a-decimal (exponente) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| Valor decimal | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
En este número binario, cada bit tiene un valor de 1, por lo que se suman todos los valores individuales.
Así, para este número, el valor decimal es el siguiente:
1 + 2 + 4 + 8 + 16+ 32 + 64 +128 = 255
Representación de números decimales en formato binario
Como ya se ha mencionado, el sistema de numeración binario sólo funciona con 1s y 0s. Sin embargo, la posición de sólo estos dos dígitos puede representar muchos más números. Los ejemplos de la sección anterior muestran cómo cualquier número decimal del 0 al 255 puede representarse utilizando números binarios. Los números mayores que 255 también pueden representarse añadiendo más bits a un número binario de 8 bits.
A continuación se muestran los números decimales del cero al 20 y sus equivalentes binarios.
| Número decimal | Número binario | Número decimal | Número binario |
|---|---|---|---|
| 0 | 0 | 11 | 1011 |
| 1 | 1 | 12 | 1100 |
| 2 | 10 | 13 | 1101 |
| 3 | 11 | 14 | 1110 |
| 4 | 100 | 15 | 1111 |
| 5 | 101 | 16 | 10000 |
| 6 | 110 | 17 | 10001 |
| 7 | 111 | 18 | 10010 |
| 8 | 1000 | 19 | 10011 |
| 9 | 1001 | 20 | 10100 |
| 10 | 1010 | — | — |
Convertir números binarios en caracteres de texto
Los números binarios pueden convertirse en caracteres de texto utilizando los códigos ASCII (American Standard Code for Information Interchange) para almacenar información en la memoria RAM o en la CPU del ordenador. Las aplicaciones compatibles con ASCII, como los procesadores de texto, pueden leer información de texto de la RAM o la CPU. También pueden almacenar información de texto que el usuario puede recuperar posteriormente. Los códigos ASCII se almacenan en la tabla ASCII, que consta de 128 caracteres de texto o especiales. Cada carácter tiene un valor decimal asociado.
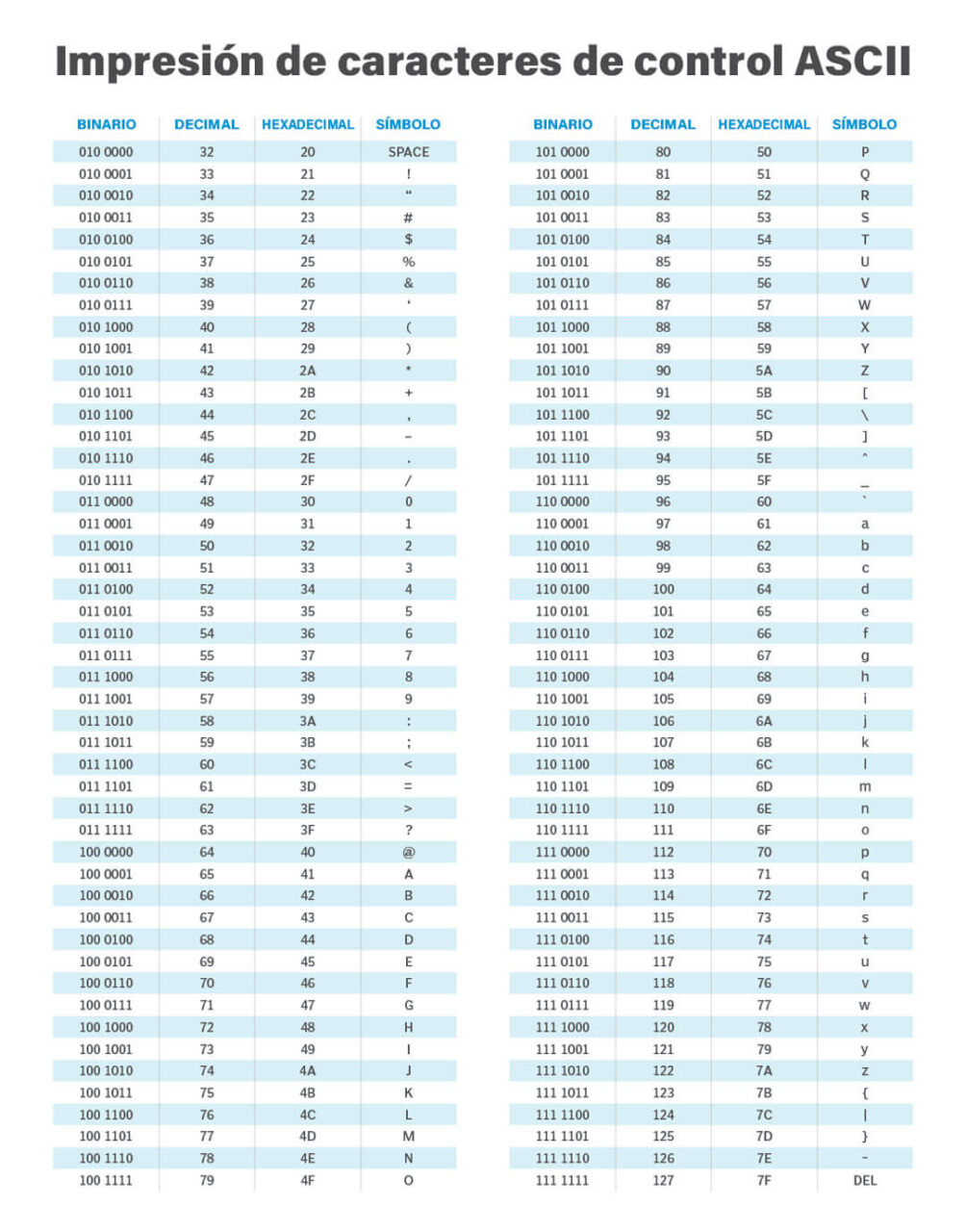
En el primer ejemplo de la sección anterior, el número binario es 01101000 (número decimal 104). En ASCII, este número produciría h minúscula. Para formar palabras, hay que añadir más letras a h. En términos binarios, esto significa añadir más números binarios al número binario de h.
Ejemplo
El código binario de la i minúscula ASCII es 01101001. Por lo tanto, para crear la palabra hi, el número binario de i se añade al número binario de h. Esto da como resultado el siguiente número binario:
01101000 + 01101001 = 0110100001101001
En términos decimales, los números decimales para h e i son 104 y 105, respectivamente.
Otros ejemplos comunes de números binarios convertidos a código de texto ASCII son los siguientes.
| Número binario | Número decimal | Código ASCCI |
|---|---|---|
| 110000 | 48 | 0 |
| 1000001 | 65 | A (mayúscula) |
| 1111111 | 127 | tecla SUPR |
| 11011 | 27 | Tecla ESC |

Deja una respuesta