La impedancia, una cantidad compleja que combina resistencia y reactancia, indica la oposición al flujo de corriente en los circuitos de CA, incorporando resistores, condensadores e inductores, al tiempo que tiene en cuenta la diferencia de fase entre voltaje y corriente.
Es fundamental para garantizar una transmisión de señal de alta calidad y un uso eficiente de la energía en varios dispositivos. Específicamente, la adaptación de impedancia es clave para minimizar la pérdida de señal y mejorar el rendimiento del equipo, lo que la convierte en una habilidad fundamental en el diseño de circuitos electrónicos.
¿Qué es la Impedancia?
La impedancia eléctrica, o simplemente impedancia, es una expresión de la oposición que un componente, circuito o sistema electrónico ofrece a la corriente eléctrica alterna y/o continua. El símbolo de la impedancia es ‘Z’ y su unidad es ‘Ohm (Ω)’, igual que en los circuitos de corriente continua (CC).
La impedancia es una magnitud vectorial (bidimensional) formada por dos fenómenos escalares (unidimensionales) independientes: la resistencia y la reactancia.
La resistencia, denotada por R, es una medida del grado en que una sustancia se opone al movimiento de electrones entre sus átomos. Cuanto más fácilmente cedan y/o acepten electrones los átomos, menor será la resistencia, que se expresa en ohmios reales positivos. La resistencia se observa con corriente alterna (CA) y también con corriente continua (CC). Ejemplos de materiales con baja resistencia, conocidos como conductores eléctricos, son el cobre, la plata y el oro. Las sustancias con alta resistencia se denominan aislantes o dieléctricas, e incluyen materiales como el polietileno, la mica y el vidrio. Un material con un nivel intermedio de resistencia se clasifica como semiconductor. Algunos ejemplos son el silicio, el germanio y el arseniuro de galio.
La reactancia, denotada por X, es una expresión del grado en que un componente, circuito o sistema electrónico almacena y libera energía a medida que la corriente y la tensión fluctúan con cada ciclo de CA. La reactancia se expresa en ohmios de número imaginario. Se observa para la CA, pero no para la CC. Cuando la CA pasa a través de un componente que contiene reactancia, la energía puede almacenarse y liberarse en forma de campo magnético, en cuyo caso la reactancia es inductiva (denotada +jXL); o la energía puede almacenarse y liberarse en forma de campo eléctrico, en cuyo caso la reactancia es capacitiva (denotada –jXC). La reactancia se multiplica convencionalmente por la raíz cuadrada positiva de -1, que es el número imaginario unitario llamado operador j, para expresar Z como un número complejo de la forma R + jXL (cuando la reactancia neta es inductiva) o R – jXC (cuando la reactancia neta es capacitiva).
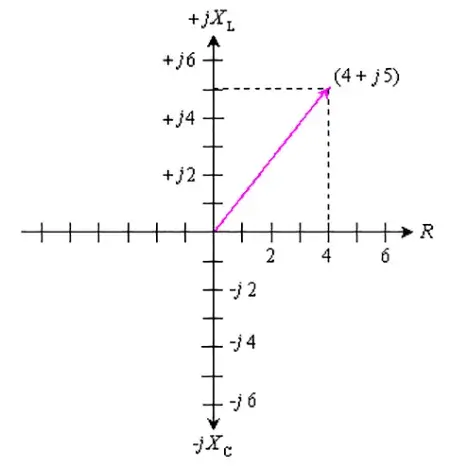
La ilustración muestra un plano de coordenadas modificado para indicar impedancias de números complejos. La resistencia aparece en el eje horizontal, moviéndose hacia la derecha (la mitad izquierda de este plano de coordenadas no se utiliza normalmente porque las resistencias negativas no se encuentran en la práctica común). La reactancia inductiva aparece en el eje imaginario positivo, moviéndose hacia arriba. La reactancia capacitiva aparece en el eje imaginario negativo, moviéndose hacia abajo. A modo de ejemplo, una impedancia compleja formada por 4 ohmios de resistencia y +j5 ohmios de reactancia inductiva se denota como un vector desde el origen hasta el punto del plano correspondiente a 4 + j5.
En los circuitos en serie, las resistencias y reactancias se suman independientemente. Supongamos que se conecta una resistencia de 100.00 ohmios en un circuito en serie con una inductancia de 10.000 ?H. A 4,0000 MHz, la impedancia compleja es:
ZRL = R + jXL = 100.00 + j251.33
Si se pone un condensador de 0.0010000 ?F en lugar del inductor, la impedancia compleja resultante a 4.0000 MHz es:
ZRC = R – jXC = 100.00 – j39.789
Si los tres componentes se conectan en serie, las reactancias se suman y se obtiene una impedancia compleja de:
ZRLC = 100 + j251.33 – j39.789 = 100 + j211.5
Esto equivale a un resistor de 100 ohmios en serie con un inductor que tiene +j211.5 ohmios de reactancia. A 4,0000 MHz, esta reactancia se presenta por una inductancia de 8.415 ?H, como se determina introduciendo los números en la fórmula para la reactancia inductiva y trabajando hacia atrás.
Los circuitos RLC en paralelo son más complicados de analizar que los circuitos en serie. Para calcular los efectos de la reactancia capacitiva e inductiva en paralelo, las cantidades se convierten en susceptancia inductiva y susceptancia capacitiva. La susceptancia es el recíproco de la reactancia. La susceptancia se combina con la conductancia, que es el recíproco de la resistencia, para formar la admitancia compleja, que es el recíproco de la impedancia compleja. Se han dedicado volúmenes enteros a los aspectos teóricos y prácticos de la resistencia, la conductancia, la reactancia, la susceptancia, la impedancia y la admitancia. Se recomienda un texto de electrónica intermedia o un libro de referencia para profundizar en el estudio.

Deja una respuesta