Las señales digitales son procesadas por el sistema digital que se puede construir con varias compuertas lógicas. Estos circuitos lógicos están hechos de varias compuertas lógicas, conectándolos en ciertas combinaciones, para producir la salida requerida. Los circuitos lógicos o circuitos digitales se clasifican principalmente en dos tipos, circuitos lógicos secuenciales y circuitos lógicos combinacionales. Este artículo da una breve idea sobre los circuitos lógicos combinacionales.
Circuitos Lógicos Combinacionales
Un circuito lógico combinacional es aquel en el que el estado actual de la combinación de las entradas lógicas decide la salida. El término lógica combinacional significa la combinación de dos o más puertas lógicas para formar una función requerida donde la salida en un momento dado depende solo de la entrada.
Las puertas lógicas son los bloques de construcción fundamentales de un circuito combinacional. Mediante el uso de la combinación de puertas lógicas se pueden implementar circuitos combinacionales más complejos como multiplexores y demultiplexores, comparadores, sumadores y restadores, etc.
Un circuito combinacional consta de variables de entrada, puertas lógicas y variables de salida. Las puertas lógicas aceptan las entradas y, según el tipo de funcionamiento de la puerta lógica, a partir de ellas se generan señales de salida.
Los datos de salida requeridos se obtienen de este proceso transformando la información binaria dada en la entrada. La siguiente figura muestra la representación esquemática de un circuito lógico combinacional generalizado que consta de n variables de entrada y m variables de salida.

En la figura anterior, hay n variables de entrada y, por lo tanto, habrá 2n posibles combinaciones de bits en la entrada. Mediante una expresión booleana de variables de entrada, se expresa cada salida. Entonces, el resultado del circuito lógico combinacional generalizado anterior se puede expresar mediante m expresiones booleanas.
En la figura anterior, el circuito acepta las variables binarias y, dependiendo de la combinación lógica de compuertas, genera salidas.
Circuitos Lógicos Combinacionales: Procedimiento de Diseño
Se puede diseñar un circuito combinacional siguiendo los siguientes pasos.
- Identificación y determinación del número de variables de entrada disponibles y variables de salida requeridas.
- Representar símbolos (alfabetos) para todas y cada una de las variables de entrada y salida.
- Expresando la relación de la variable de entrada y salida.
- Construcción de tabla de verdad que indique la relación entre las variables de entrada y salida.
- Obtención de la expresión booleana para cada variable de salida en términos de variables de entrada.
- Minimizar las expresiones booleanas de varias variables de salida.
- Obtención del diagrama lógico mediante la implementación de expresiones booleanas minimizadas.
Para minimizar las expresiones booleanas, se encuentran disponibles varias técnicas de simplificación para reducir el número de compuertas y, por lo tanto, reducir el costo de implementación. Estas técnicas incluyen teoremas e identidades del álgebra booleana, mapas de Karnaugh (mapas K), tabulación de Quinne-McCluskey, etc. Para la implementación de hardware del circuito combinacional, se prefieren las siguientes pautas.
- La implementación del circuito debe ser tal que, tenga un número mínimo de compuertas, teniendo un número mínimo de entradas.
- El número de interconexiones entre las compuertas debería ser mínimo y el tiempo de propagación debería ser el mínimo.
- Siempre debe haber una limitación en la capacidad de conducción de las compuertas.
Este es el método simple, efectivo y tradicional de diseñar un circuito combinacional para circuitos pequeños. Si el circuito es más complejo, la cantidad de compuertas requeridas es mayor y también requiere una mayor cantidad de cables entre ellas. Por lo tanto, diseñar tales circuitos puede ser menos confiable y requerir más tiempo.
Para superar estos problemas, la mayoría de los circuitos combinacionales están disponibles en circuitos integrados (CI) que se utilizan ampliamente en el diseño de sistemas digitales. Depende de la capacidad de integración de las compuertas, estos circuitos integrados se clasifican en circuitos integrados de pequeña, mediana, grande y muy grande escala.
Para realizar funciones digitales específicas tales como adición, multiplexación, demultiplexación, codificación, decodificación, comparación, etc., en los sistemas digitales se utilizan principalmente circuitos integrados de escala media integrada (MSI).
Funciones del Circuito Lógico Combinacional
La función de los circuitos lógicos combinacionales se puede especificar de tres formas principales, tales como:
Existen tres formas principales de especificar la función de un circuito lógico combinacional, estos son:
- Tabla de Verdad
- Álgebra Booleana
- Diagrama Lógico
Tabla de Verdad
Una tabla de verdad define la función de una compuerta lógica al proporcionar una lista concisa que muestra todos los estados de salida en forma de tabla para cada combinación posible de variable de entrada que la compuerta podría encontrar.

Álgebra Booleana
Esto forma la expresión algebraica que muestra el funcionamiento del circuito lógico para cada variable de entrada, ya sea Verdadero o Falso, que da como resultado una salida lógica “1”.
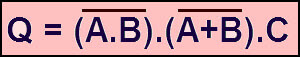
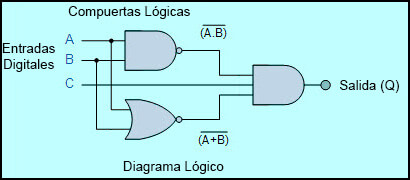
Diagrama Lógico
Esta es una representación gráfica de un circuito lógico que muestra el cableado y las conexiones de cada compuerta lógica individual, representada por un símbolo gráfico específico, que implementa el circuito lógico.
Los circuitos lógicos combinacionales también pueden denominarse circuitos de toma de decisiones, ya que están diseñados utilizando compuertas lógicas individuales. La lógica combinacional es el proceso de combinar compuertas lógicas para procesar las dos o más entradas dadas de manera que se genere al menos una señal de salida basada en la función lógica de cada compuerta lógica.
Ejemplo de Circuito Lógico Combinacional
Declaración: Diseñe un circuito lógico combinacional con tres variables de entrada de modo que produzca una salida lógica 1 cuando una o dos de las variables de entrada sean lógicas 1 pero no las tres.
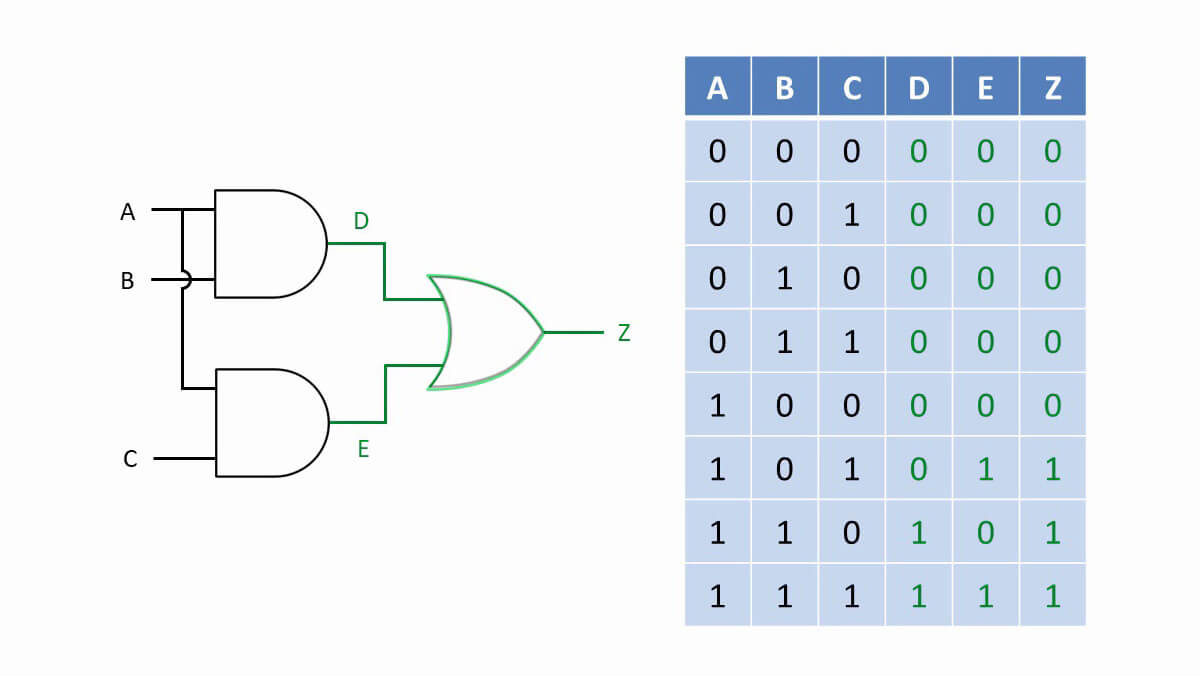
Solución: Siga los puntos enumerados anteriormente para diseñar el diagrama lógico según la declaración dada. En la declaración dada hay tres variables de entrada y una variable de salida. Como segundo paso, asigne las variables de entrada con símbolos de letras como A, B, C y la salida como Y. A continuación, la relación entre las variables de entrada y salida se puede tabular construyendo la tabla de verdad como se indica a continuación.
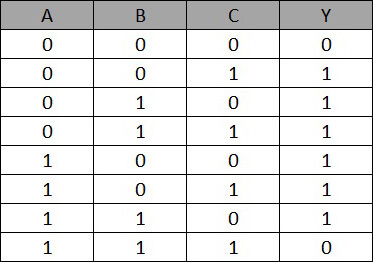
Ahora, la expresión booleana simplificada para la tabla de verdad anterior para obtener la salida Y se obtiene usando la simplificación del mapa K como
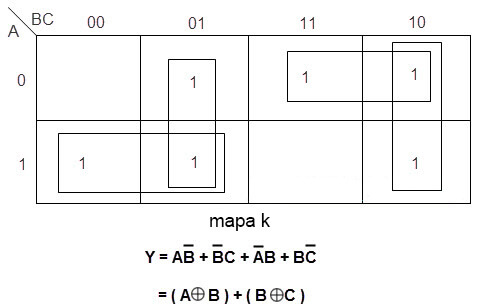
Al implementar la ecuación booleana anterior, obtenemos el diagrama lógico como
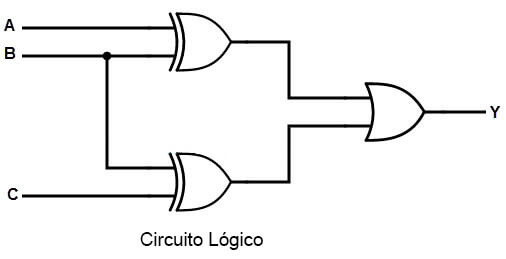
Clasificación de los Circuitos Lógicos Combinacionales
Los circuitos combinacionales se utilizan en una amplia variedad de aplicaciones que incluyen calculadoras, técnicas de medición digital, computadoras, procesamiento digital, control automático de máquinas, procesamiento industrial, comunicaciones digitales, etc.
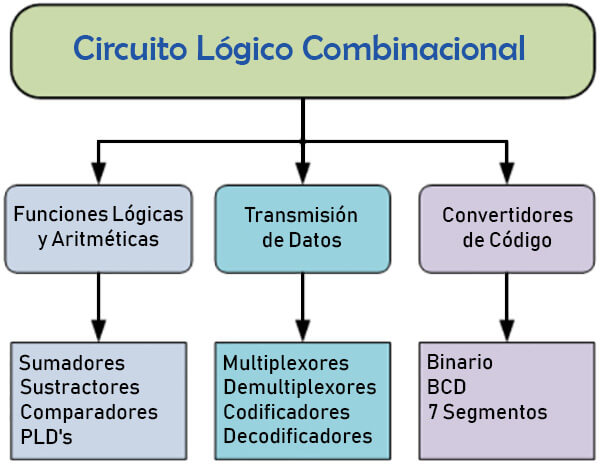
Se utilizan diferentes tipos de circuitos lógicos combinacionales para diversas aplicaciones. Dependiendo de la función del circuito lógico empleado, los circuitos lógicos combinacionales se clasifican principalmente en tres tipos, estos son, circuitos aritméticos y lógicos, circuitos de transmisión de datos y circuitos convertidores de código.
Circuitos Aritméticos y Lógicos
Las operaciones aritméticas son una de las principales funcionalidades de la mayoría de las computadoras y calculadoras. Estas operaciones son realizadas por las compuertas lógicas o simplemente circuitos combinacionales que combinan las varias compuertas lógicas para realizar la función requerida. Estas funcionalidades aritméticas de los circuitos combinacionales incluyen suma, resta, multiplicación, etc.
Algunos de los circuitos combinacionales utilizados para estas operaciones son Semisumador, Sumador completo, Semirestador, Resta completa, Sumador-Restador, Comparadores, PLD (Dispositivos lógicos programables), etc.
Circuitos de Transmisión de Datos
Los circuitos combinacionales más utilizados son los multiplexores y demultiplexores. Un circuito lógico multiplexor acepta las diversas entradas de datos y pasa una de ellas a través de la salida a la vez. Estos se utilizan en aplicaciones de selección de datos, conversión en paralelo a serie, enrutamiento de datos en sistemas digitales.
Un circuito demultiplexor realiza la operación inversa a la del multiplexor. Acepta la entrada única y la distribuye a múltiples salidas. Estos se utilizan en distribuidores, así como en aplicaciones de convertidores de serie a paralelo.
Otros circuitos de transmisión de datos esenciales incluyen codificadores y decodificadores. Un circuito lógico decodificador convierte el código de entrada binario de n bits en 2n líneas de salida. Cada línea de salida se activa solo para una de las posibles combinaciones de las entradas.
Estos se utilizan en la demultiplexación de datos, convertidores de digital a analógico y aplicaciones de visualización digital. Un circuito digital codificador convierte una señal de entrada activa en una señal de salida codificada como operación inversa del decodificador. Se utilizan en aplicaciones de compresión de bits.
Circuitos Convertidores de Código
En algunas aplicaciones, es necesario interconectar dos bloques digitales de diferentes sistemas de codificación. Entonces, se usa un circuito de conversión entre dichos circuitos para convertir la información. Algunos de estos convertidores son de código binario a código gray, código gray a binario, BCD a código de exceso 3, código de exceso 3 a código BCD y circuitos de conversión de código de siete segmentos.
Deja una respuesta